Im Internet
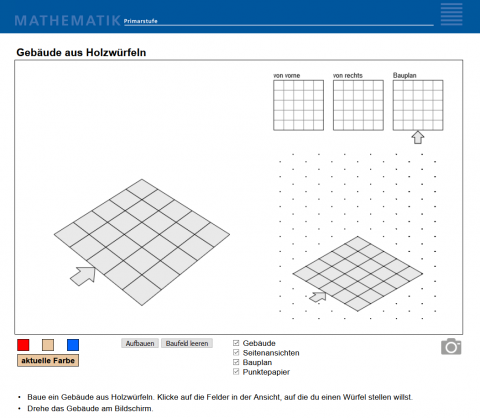
Gebäude aus Holzwürfeln
Online-AnwendungDie Lernenden bauen Gebäude aus Holzwürfeln. Die Gebäude werden mit verschiedenen Ansichten verglichen. Die Ansichten können ausgeblendet werden, so dass die Lernenden die fehlenden Ansichten auf Papier aufzeichnen und anschliessend durch das Einblenden der Ansicht kontrollieren können, ob ihre Arbeit korrekt ist.

Würfelgebilde
Online-AnwendungDie Lernenden sehen ein Würfelgebäude mit drei Bauplänen dazu. Sie sollen entscheiden, welcher Bauplan zum Würfelgebäude passt.

Würfelgebäude - 3x3x3
Online-AnwendungDie Aufgaben basieren auf einem grossen Würfel, der aus 27 kleinen besteht (3x3x3). Diesen Würfel kann man als Orientierungshilfe anzeigen lassen, indem man den Mauszeiger über die Grafik hält. Die Anwendung beinhaltet drei Aufgabenstellungen:
- Würfel zählen: Die Anzahl Würfel des Würfelgebäudes werden gezählt.
- Würfel ergänzen: Lernende berechnen die Anzahl Würfel, die noch zu ergänzen sind, um den grossen Würfel komplett zu füllen.
- Bauplan erstellen: Lernende betrachten den Würfel von oben und notieren, wo wie viele Würfel übereinander liegen.
Tipp: Wenn möglich den Link mit den Browsern Firefox oder Chrome öffnen; dadurch wird keine Werbung angezeigt.
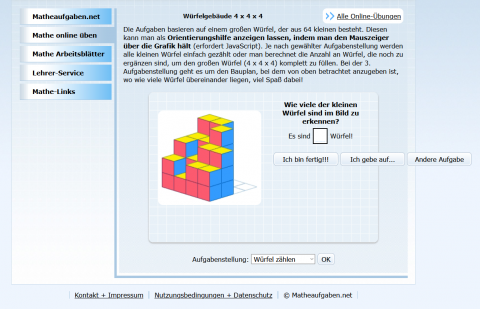
Würfelgebäude - 4x4x4
Online-AnwendungDie Aufgaben basieren auf einem grossen Würfel, der aus 64 kleinen besteht (4x4x4). Diesen Würfel kann man als Orientierungshilfe anzeigen lassen, indem man den Mauszeiger über die Grafik hält. Die Anwendung beinhaltet drei Aufgabenstellungen:
- Würfel zählen: Die Anzahl Würfel des Würfelgebäudes werden gezählt.
- Würfel ergänzen: Lernende berechnen die Anzahl Würfel, die noch zu ergänzen sind, um den grossen Würfel komplett zu füllen.
- Bauplan erstellen: Lernende betrachten den Würfel von oben und notieren, wo wie viele Würfel übereinander liegen.
Tipp: Wenn möglich den Link mit den Browsern Firefox oder Chrome öffnen; dadurch wird keine Werbung angezeigt.
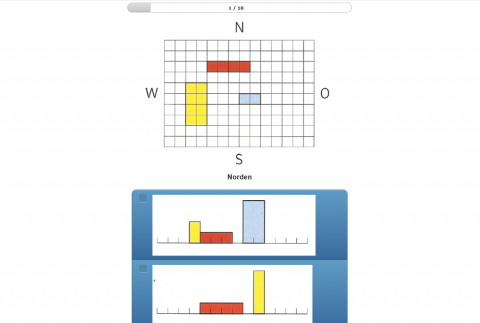
Quaderansichten
Online-AnwendungDiese Anwendung ist eine Ergänzung zum Thema "Quaderansichten" im Zahlenbuch. Die Lernenden sehen einen Grundriss, auf welchem drei Quader stehen sowie fünf vorgegebe Seitenansichten. Die Lernenden entscheiden, welche Seitenansicht zum Grundriss passt.
Anton App
Lern-App (kostenlos)Verschiedene Inhalte der Geometrie werden in der Anton App von der 1. bis 9. Klasse behandelt. Die App steht kostenlos zur Verfügung. Um die App nutzen zu können, braucht es eine Anmeldung. Eine detaillierte Startanleitung findet sich unten. Die App bietet die Möglichkeit, eine Schulklasse anzulegen, Aufgaben zuzuweisen und Lernfortschritte der Lernenden zu verfolgen.
Die Anton App bietet nicht nur zahlreiche Übungen zum Thema Geometrie, sondern hat auch eine grosse Auswahl an Übungen zu allen anderen Fächern des Lehrplan 21.
Auf Papier
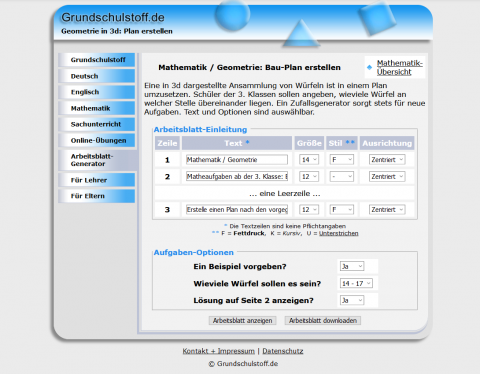
Würfelgebäude - Bauplan erstellen
Arbeitsblatt-GeneratorEin Zufallsgenerator generiert Arbeitsblätter, auf welchen Würfelgebäude abgebildet sind. Die Lernenden sollen die Baupläne zu den Würfelgebäuden ergänzen. Die Arbeitsblätter können mit oder ohne Lösung erstellt werden.
Tipp: Wenn möglich den Link mit den Browsern Firefox oder Chrome öffnen; dadurch wird keine Werbung angezeigt.
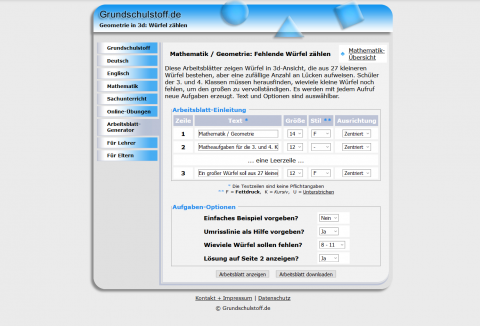
Würfelgebäude - fehlende Würfel zählen
Arbeitsblatt-GeneratorDiese Arbeitsblätter zeigen Würfel, die aus 27 kleineren Würfel bestehen, aber eine zufällige Anzahl an Lücken aufweisen. Lernende müssen herausfinden, wie viele kleine Würfel noch fehlen, um den grossen zu vervollständigen. Es werden mit jedem Aufruf neue Aufgaben erzeugt. Text und Optionen sind auswählbar.
Tipp: Wenn möglich den Link mit den Browsern Firefox oder Chrome öffnen; dadurch wird keine Werbung angezeigt.
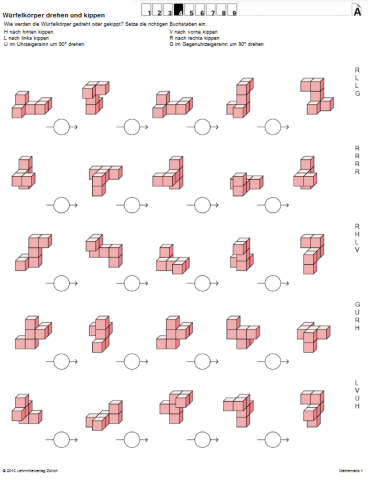
Würfelkörper drehen und kippen
ArbeitsblattDie Lernenden entscheiden, in welche Richtung vorgegebene Würfelgebäude gedreht oder gekippt wurden. Ist die Aufgabe zu anspruchsvoll, um in der Vorstellung gelöst zu werden, ist es sinnvoll, die Würfelgebäude aus kleinen Holzwürfeln nachzubauen.

Würfelkörper drehen und kippen
ArbeitsblattDie Lernenden stellen sich die Drehung oder Kippung in Gedanken vor und skizziere den Würfelkörper in der neuen Lage. Ist die Aufgabe zu anspruchsvoll, um in der Vorstellung gelöst zu werden, ist es sinnvoll, die Würfelgebäude aus kleinen Holzwürfeln nachzubauen.
Spiele

Potz Klotz - ein raumgeometrisches Spiel
1. und 2. ZyklusAus fünf Holzwürfeln wird ein Würfelgebäude errichtet. Alle Mitspielenden erhalten eine vereinbarte Anzahl von Karten, auf welchen verschiedene Würfelgebäude aus fünf Würfeln abgebildet sind. Reihum versuchen die Spielenden das Gebäude durch Umlegen von nur einem Würfel so umzubauen, dass es der Abbildung auf einer ihrer Karten entspricht. (Quelle: Verlag)

Spiele mit dem Somawürfel
2. ZyklusUnregelmässige Körper, die aus höchstens 4 Würfeln bestehen, werden richtig zusammengesetzt, damit sich wieder ein Würfel ergibt.

Somawürfel-Quartett: Kopfgeometrie mit dem Somawürfel
2. ZyklusBeim Somawürfel-Quartett werden spielerisch kopfgeometrische Fähigkeiten gefördert. Die zentrale Aufgabe besteht darin, Quartette von Tierfiguren, die aus Somawürfel-Teilen gebildet sind, zu vervollständigen. (Quelle: Verlag)

Schauen und Bauen
2. ZyklusIm ersten Spiel geht es bei jeder der 40 Aufgaben darum, drei Quader in unterschiedlicher Lage vier vorgegebenen Seitenansichten entsprechend auf einem Grundplan aufzustellen. Der Reiz des Spieles besteht darin, dass keines der vier Kinder von seiner Seite aus die volle Information hat, um eine Aufgabe zu lösen. Die Kinder kommen nur zum Ziel, wenn sie kooperieren!
Im zweiten Spiel muss überlegt werden, wie ein Quader auf einem Gitter von einer Startposition aus durch Kippen in vorgegebene Zielpositionen befördert werden kann. Gefordert ist hier vorausschauendes Denken! (Quelle: Verlag)

Architecto
1. und 2. ZyklusAus verschiedenen geometrischen Formen werden Bauwerke errichtet. Am Anfang noch einfach, entwickelt sich architecto von Aufgabe zu Aufgabe zu einer grösseren Herausforderung, denn pro Aufgabe darf nur eine bestimmte Zahl von Bausteinen verwendet werden - und keiner soll übrig bleiben. (Quelle: Verlag)

Cubus
2. ZyklusNach festen Regeln bauen die Lernenden gemeinsam einen Kistenstapel. Durch geschicktes Bauen, Umbauen und Beobachten des Kistenstapels sowie der Rauten der Mitspielenden versucht jede Person, möglichst viele Punkte zu erhalten. Wer am Ende die meisten hat, gewinnt. (Quelle: Verlag)